ECUACIONES DIFERENCIALES

Ecuación diferencial

Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:

• Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
• Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.

  Ecuación diferencial lineal

  Se dice que una ecuación es lineal si tiene la forma , es decir:
  
• Ni la función ni sus derivadas están elevadas a ninguna potencia distinta de uno o cero.
• En cada coeficiente que aparece multiplicándolas sólo interviene la variable independiente.
• Una combinación lineal de sus soluciones es también solución de la ecuación.

Ejemplos:

• es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones , con k un número real cualquiera.
• es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones , con a y b reales.
• es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones , con a y b reales.

Usos

Las ecuaciones diferenciales son muy utilizadas en todas las ramas de la ingeniería para el modelado de fenómenos físicos. Su uso es común tanto en ciencias aplicadas, como en ciencias fundamentales (física, química, biología) o matemáticas, como en economía.

• En dinámica estructural, la ecuación diferencial que define el movimiento de una estructura es:

Donde M es la matriz que describe la masa de la estructura, C es la matriz que describe el amortiguamiento de la estructura, K es la matriz de rigidez que describe la rigidez de la estructura, x es vector de desplazamientos [nodales] de la estructura, P es el vector de fuerzas (nodales equivalentes), y t indica tiempo. Esta es una ecuación de segundo orden debido a que se tiene el desplazamiento x y su primera y segunda derivada con respecto al tiempo.

• La vibración de una cuerda está descrita por la siguiente ecuación diferencial en derivadas parciales de segundo orden:

• 

donde es el tiempo y es la coordenada del punto sobre la cuerda y una constante que corresponde a la velocidad de propagación de dicha onda. A esta ecuación se le llama ecuación de onda.

Ecuaciones semilineales y cuasilineales

No existe un procedimiento general para resolver ecuaciones diferenciales no lineales. Sin embargo, algunos casos particulares de no linealidad sí pueden ser resueltos. Son de interés el caso semilineal y el caso cuasilineal.
Una ecuación diferencial ordinaria de orden n se llama cuasilineal si es "lineal" en la derivada de orden n. Más específicamente, si la ecuación diferencial ordinaria para la función puede escribirse en la forma:

Se dice que dicha ecuación es cuasilineal si es una función afín, es decir, .
Una ecuación diferencial ordinaria de orden n se llama semilineal si puede escribirse como suma de una función "lineal" de la derivada de orden n más una función cualquiera del resto de derivadas. Formalmente, si la ecuación diferencial ordinaria para la función puede escribirse en la forma:

Se dice que dicha ecuación es semilineal si es una función lineal.

Solución de una ecuación diferencial

Tipos de soluciones

Una solución de una ecuación diferencial es una función que al reemplazar a la función incógnita, en cada caso con las derivaciones correspondientes, verifica la ecuación, es decir, la convierte en una identidad. Hay tres tipos de soluciones:

1. Solución general: una solución de tipo genérico, expresada con una o más constantes.

Solución general

Es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes (una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc). En caso de que la ecuación sea lineal, la solución general se logra como combinación lineal de las soluciones (tantas como el orden de la ecuación) de la ecuación homogénea (que resulta de hacer el término no dependiente de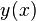 ni de sus derivadas igual a 0) más una solución particular de la ecuación completa.

1. Solución particular: Si fijando cualquier punto por donde debe pasar necesariamente la solución de la ecuación diferencial, existe un único valor de C, y por lo tanto de la curva integral que satisface la ecuación, éste recibirá el nombre de solución particular de la ecuación en el punto , que recibe el nombre de condición inicial.

Solución particular

Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.

1. Solución singular: una función que verifica la ecuación, pero que no se obtiene particularizando la solución general.

Solución singular

Solución de la ecuación no consistente en una particular de la general.

Resolución de algunas ecuaciones

• Ecuación diferencial de primer orden
• Ecuación diferencial lineal
• Ecuación diferencial exacta
• Ecuación de Jacobi
• Ecuación de Clairaut y también se llaman ecuaciones de estado diferencial que como las ecuaciones lineales de dos variables, éstas son tangentes.