La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La anti-derivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
Notación
La notación que emplearemos para referirnos a una anti-derivada es la siguiente:
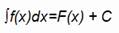
Teorema
Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.
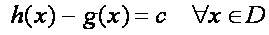
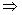
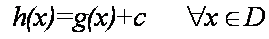
Conclusión: Si g(x) es una antiderivada de f en un conjunto D de números reales, entonces cualquier antiderivada de f es en ese conjunto D se puede escribir como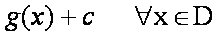
c constante real.
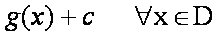c constante real.
Fórmula que relaciona la integral definida y la indefinida
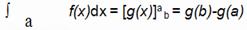
A la hora de resolver una antiderivada o integral indefinida se deben tener disponibles los recursos aritméticos y heurísticos. Estos son:
- Concepto.
- Propiedades.
- Reglas de integración.
- Integrales inmediatas.
- Métodos clásicos de integración:
-Integración por sustitución.
-Integración por partes.
-Integración de fracciones racionales mediante fracciones simples.
- Uso de tablas.
- Integración de funciones trigonométricas sencillas.
- Integración de funciones racionales sencillas.
No hay comentarios:
Publicar un comentario