Ecuación diferencial
Una
ecuación diferencial es una ecuación en la que intervienen derivadas
de una o más funciones desconocidas. Dependiendo del número de
variables independientes respecto de las que se deriva, las ecuaciones
diferenciales se dividen en:
- Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
- Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
Ecuación diferencial lineal
Se dice que una ecuación es lineal si tiene la forma  , es decir:
, es decir:
- Ni la función ni sus derivadas están elevadas a ninguna potencia distinta de uno o cero.
- En cada coeficiente que aparece multiplicándolas sólo interviene la variable independiente.
- Una combinación lineal de sus soluciones es también solución de la ecuación.
Ejemplos:
 es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones  , con k un número real cualquiera.
, con k un número real cualquiera. es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones  , con a y b reales.
, con a y b reales. es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones  , con a y b reales.
, con a y b reales.
Usos
Las ecuaciones diferenciales son muy utilizadas en todas las ramas de la
ingeniería para el modelado de fenómenos físicos. Su uso es común tanto en
ciencias aplicadas, como en ciencias fundamentales (
física,
química,
biología) o
matemáticas, como en
economía.

Donde
M es la
matriz que describe la
masa de la estructura,
C es la matriz que describe el
amortiguamiento de la estructura,
K es la
matriz de rigidez que describe la
rigidez de la estructura,
x es vector de desplazamientos [nodales] de la estructura,
P es el vector de fuerzas (nodales equivalentes), y
t indica tiempo. Esta es una ecuación de segundo orden debido a que se tiene el desplazamiento
x y su primera y segunda derivada con respecto al tiempo.
- La vibración de una cuerda está descrita por la siguiente ecuación diferencial en derivadas parciales de segundo orden:
donde
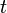
es el tiempo y

es la coordenada del punto sobre la cuerda y

una constante que corresponde a la velocidad de propagación de dicha onda. A esta ecuación se le llama ecuación de onda.
Ecuaciones semilineales y cuasilineales
No existe un procedimiento general para resolver ecuaciones diferenciales no lineales.
Sin embargo, algunos casos particulares de no linealidad sí pueden ser
resueltos. Son de interés el caso semilineal y el caso cuasilineal.
Una ecuación diferencial ordinaria de orden
n se llama cuasilineal si es "lineal" en la derivada de orden
n. Más específicamente, si la ecuación diferencial ordinaria para la función

puede escribirse en la forma:

Se dice que dicha ecuación es cuasilineal si

es una función afín, es decir,

.
Una ecuación diferencial ordinaria de orden
n se llama semilineal si puede escribirse como suma de una función "lineal" de la derivada de orden
n más una función cualquiera del resto de derivadas. Formalmente, si la ecuación diferencial ordinaria para la función

puede escribirse en la forma:
Se dice que dicha ecuación es semilineal si

es una función lineal.
Solución de una ecuación diferencial
Tipos de soluciones
Una solución de una ecuación diferencial es una función que al
reemplazar a la función incógnita, en cada caso con las derivaciones
correspondientes, verifica la ecuación, es decir, la convierte en una
identidad. Hay tres tipos de soluciones:
- Solución general: una solución de tipo genérico, expresada con una o más constantes.
Solución general
Es un haz de curvas. Tiene un orden de infinitud de acuerdo a su
cantidad de constantes (una constante corresponde a una familia
simplemente infinita, dos constantes a una familia doblemente infinita,
etc). En caso de que la ecuación sea lineal, la solución general se
logra como combinación lineal de las soluciones (tantas como el orden de
la ecuación) de la ecuación homogénea (que resulta de hacer el término
no dependiente de
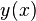
ni de sus derivadas igual a 0) más una solución particular de la ecuación completa.
- Solución particular: Si fijando cualquier punto
 por donde debe pasar necesariamente la solución de la ecuación
diferencial, existe un único valor de C, y por lo tanto de la curva
integral que satisface la ecuación, éste recibirá el nombre de solución
particular de la ecuación en el punto
por donde debe pasar necesariamente la solución de la ecuación
diferencial, existe un único valor de C, y por lo tanto de la curva
integral que satisface la ecuación, éste recibirá el nombre de solución
particular de la ecuación en el punto  , que recibe el nombre de condición inicial.
, que recibe el nombre de condición inicial.
Solución particular
Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.
- Solución singular: una función que verifica la ecuación, pero que no se obtiene particularizando la solución general.
Solución singular
Solución de la ecuación no consistente en una particular de la general.
Resolución de algunas ecuaciones




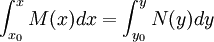

 o
o 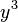 en función de qué cambio haga más simple su resolución. Llegados a este caso según la elección se puede optar por uno de los dos cambios análogos, que son:
en función de qué cambio haga más simple su resolución. Llegados a este caso según la elección se puede optar por uno de los dos cambios análogos, que son: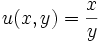 o bien
o bien 



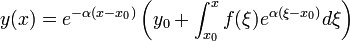
 y
y  , la solución es:
, la solución es:

![y(x)={\frac {{e^{-\int \!P \left( x \right) {dx}}}}{\sqrt [\alpha-1]{ \left( 1-\alpha \right) \int \!Q \left( x \right) {e^{
\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}}{dx}+C}}}](http://upload.wikimedia.org/math/9/a/4/9a47238d1aa4d74ae68a27dd1f66ea05.png)
![v(x) = [y(x)]^{(1-\alpha)}](http://upload.wikimedia.org/math/5/a/d/5ad96c3cb0277f5fd03823a426704314.png)


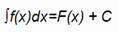
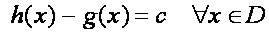
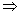
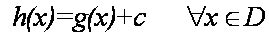
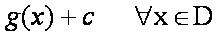 c constante real.
c constante real.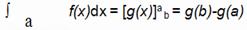
 , es decir:
, es decir: es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones  , con k un número real cualquiera.
, con k un número real cualquiera. es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones  , con a y b reales.
, con a y b reales. es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones
es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones  , con a y b reales.
, con a y b reales.

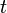 es el tiempo y
es el tiempo y  es la coordenada del punto sobre la cuerda y
es la coordenada del punto sobre la cuerda y  una constante que corresponde a la velocidad de propagación de dicha onda. A esta ecuación se le llama ecuación de onda.
una constante que corresponde a la velocidad de propagación de dicha onda. A esta ecuación se le llama ecuación de onda. puede escribirse en la forma:
puede escribirse en la forma: es una función afín, es decir,
es una función afín, es decir,  .
. es una función lineal.
es una función lineal.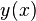 ni de sus derivadas igual a 0) más una solución particular de la ecuación completa.
ni de sus derivadas igual a 0) más una solución particular de la ecuación completa. por donde debe pasar necesariamente la solución de la ecuación
diferencial, existe un único valor de C, y por lo tanto de la curva
integral que satisface la ecuación, éste recibirá el nombre de solución
particular de la ecuación en el punto
por donde debe pasar necesariamente la solución de la ecuación
diferencial, existe un único valor de C, y por lo tanto de la curva
integral que satisface la ecuación, éste recibirá el nombre de solución
particular de la ecuación en el punto